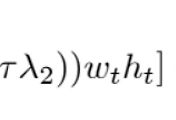another derivation steady state

And using the facts from last time (dropping t, t+1 and having ht+1 = ht):

 

\[ \frac{\beta \theta_2}{\mu_2 e} = R [(1-\tau \lambda_2)nwh] - [\tau_2 (1-\Omega)\frac{wh\beta n}{e}] \]

multiplying e to both sides, and taking nwh out:

\[ \frac{\beta \theta_2}{\mu_2} = whn([R(1-\tau \lambda_2) e] - [\tau_2 (1-\Omega)\beta]) \]

Note that \(\frac{\rho}{c_2} = \mu_2 w h \), meaning that \(wh = \frac{\rho}{\mu_2 c_2} \)

\[ \frac{\beta \theta_2}{\mu_2} = \frac{\rho}{\mu_2 c_2}n([R(1-\tau \lambda_2) e] - [\tau_2 (1-\Omega)\beta]) \]

muliply \(c_2 \mu_2\) on both sides, we get

\[ \beta \theta_2 c_2 = \rho n([R(1-\tau \lambda_2) e] - [\tau_2 (1-\Omega)\beta]) \]

which is equivalent to

\[ \beta \theta_2 c_2 = \rho e R(1-\tau \lambda_2)n - \rho \tau_2 (1-\Omega)\beta n \]

 

which is the result we want!

the result we want