Deriving steady state equation (ft. latex)

We start from this equation:

 

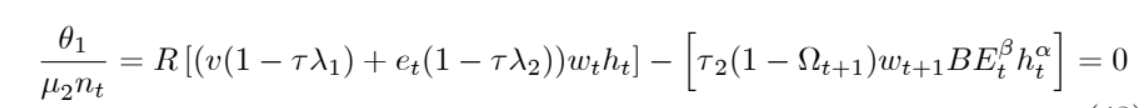
And we wish to get to (under steady state* assumption)

 

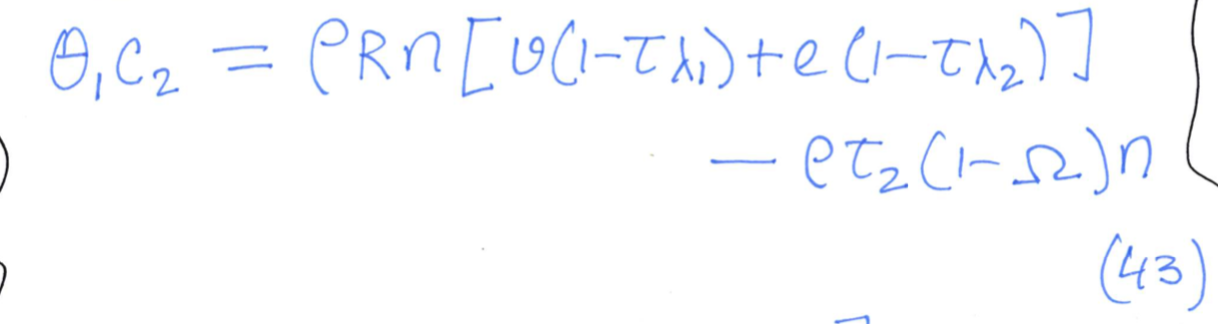
*note: in steady state, 't' and 't+1' can be removed. eg \(h_t\) and \(h_{t+1}\) are equivalent so we can instead use \(h\) for both

 

Before we get started, I'll denote the following as 'STUFF', as we want to preserve that part anyway:

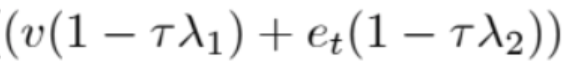
Likewise, \(\tau_2(1-\Omega_{t+1})\) will be denoted as 'STUFF2'

Further, as noted in the previous article, \(h_{t+1} = B E_t^\beta h_t^\alpha\), so I'll assume that substitution is made.

Let's start by rewriting the original equation.

 

\[ \frac{\theta_1}{\mu_2 n} = R[STUFF \times w h] - [STUFF2 w h] \]

 

(Note we want to get to \( \theta_1 c_2 = \rho R n \times [STUFF] - \rho n \times [STUFF2]\))

multiply \(\mu_2 n\) on both sides, which will yield:

\[\theta_1 =\mu_2 n (R[STUFF \times w h] - [STUFF2 \times w h] )\] 

Then 

\[\theta_1 =\mu_2 n w h (R[STUFF] - [STUFF2] )\] 

Use the following fact to replace wh:

fact1 (don't forget SS condition, where you drop t and t+1)

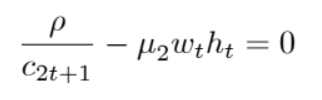
Meaning the equation is now:

\[\theta_1 =\frac{\rho \mu_2 n}{c_2 \mu_2} \times (R[STUFF] - [STUFF2] )\] 

This simplifies to

\[\theta_1 =\frac{\rho n}{c_2} \times (R[STUFF] - [STUFF2] )\] 

and multiplying both sides by \(c_2\),

\[\theta_1 c_2 =\rho n \times (R[STUFF] - [STUFF2] )\] 

expanding it,

\[\theta_1 c_2 =\rho n R[STUFF] - \rho n[STUFF2] )\] 

which is equivalent to 

\[ \theta_1 c_2 = \rho R n [STUFF] - \rho n [STUFF2] \]

That we wanted to get at the start!