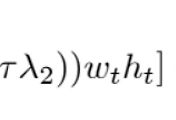Modelling utility of a person over 2 phases of ages

Ultimately, we get to

\[U(c_{1t}, c_{2t+1},h_{t+1}) = \ln{C_{1t}} + \rho lnC_{2t+1} + \theta ln h_{t+1}\]

 

Suppose we model a person's utility function. How do we do that? We may start from a very simple principle; that is, a person's utility is a function of their consumption.

 

\[U(consumption) = consumption\]

 

We can make this more elaborated, by considering the fact that a person's marginal utility (utility gained for each additional conusumption) declines over time. This is often modelled by a logarithmic function. The rationale behind that is that both log(x) and x are strictly increasing at evaluated values above (or equal to) 0 when x starts from 1, so behaviour of y = x is preserved (strictly increasing) when y = log(x) is used. However, when we use y = log(x), we also take account of the strictly decreasing slope (implied by decreasing marginal utility). So our model is now:

 

\[U(consumption) = ln{consumption}\] 

 

Where did the \(t\) in the first equation come from? It's the consequence of the following notations:

\[

\begin{itemize}

\item t: when a person is at an (young) adult age 

\item t+1: when a person is at an old age where they receive pension

\end{itemize}

\]

 

so '1' in t+1 is just the length of period between when a person is young and when they are old. Let's denote \(c_{1 t} as the consumption at young age, c_{2 t+1} as consumption at older age.

 

We can say that the utility that a person gets is the sum of how much they consume when they are young, and how much they earn when they are older; so equation is now:

 

\[U(c_{1t}, c_{2t+1},h_{t+1}) = \ln{C_{1t}} + \rho lnC_{2t+1} \]

 

\(\rho\) is some random constant to denote that the utility of consumption at old age might be a constant factor diminished compared to consumption at young age (if \( 0 < \rho < 1 \) ).

 

The modelling would've more or less stopped here (barring the lagrangian constraint) if we were dealing with a very basic case. However, we consider the following situation:

 

Suppose that a person is young (still an adult, just young, and has some children). The person invests in their children, to increase the human capital of their children. The children grows older, and when the person is old as to receive a pension, they receive money from their children - now this becomes part of the equation in the utility function of the person. Note that we are ultimately trying to model a situation in which it may be the case that the fact that when children grows older they pay their parents part of their income, whether it be through their free will or some government's forcible tax scheme (PAYGO, Diamond 1962), incentivises the parents to invest in them.

 

FIrst of all, we model the resulting output of parents' investment on education of children using the standard Cobb-douglas model, where human capital is the children's human capital \(h_{t+1}\), and the inputs are parents' human capital (\(h_{t}\)and education technology \(E_{t}\) (that is, the state of education of that country that fascilitates parents' investment of their capital**). Then the model looks like:

 

**EDIT: \(E_{t}\) actually denotes the fraction of income that parents spend for children's education. You can probably think of human capital of parents \(h_{t}\) as all the other things that parents provide with their strength and resources to support their child.

 

\[h_{t+1} = B E_{t}^\beta h_{t} ^ \alpha \]

 

Note that in Cobb Douglas model, the exponent of each capital (in this case, human capital and education technology) are the elasticities of those capitals; that is, \(\alpha\) in this case will denote how much increase in children's human capital one percent increase in parent's investment of their human capital will bring about; similarly for Education.

 

We now extend this notion of investment of parents on children to how children becomes a factor of parents' utility (or happiness in their lives, yeah sounds kinda vague and cringy). Here's the equation I presented at the start.

 

\[U(c_{1t}, c_{2t+1},h_{t+1}) = \ln{C_{1t}} + \rho lnC_{2t+1} + \theta ln h_{t+1}\] 

 

The added term \( \theta ln h_{t+1} \) simply is saying that children give parents a certain percentage (\(\theta\)) of their human capital to parents.

 

Next, we will go onto some further constraints regarding this utility. The motivations for restraints arise from the simple fact that the solution to utility maximisation for such a simple equation presented at the start will simply be: infinite consumption, infinite investment (since there's no restraint to those variables). We will observe Lagrangian constraints being applied to make sure that this is balanced with their incomes.