So TODAY!!! I've done a leetcode medium problem, which has a success rate of around 36 percent (so it's quite low!)
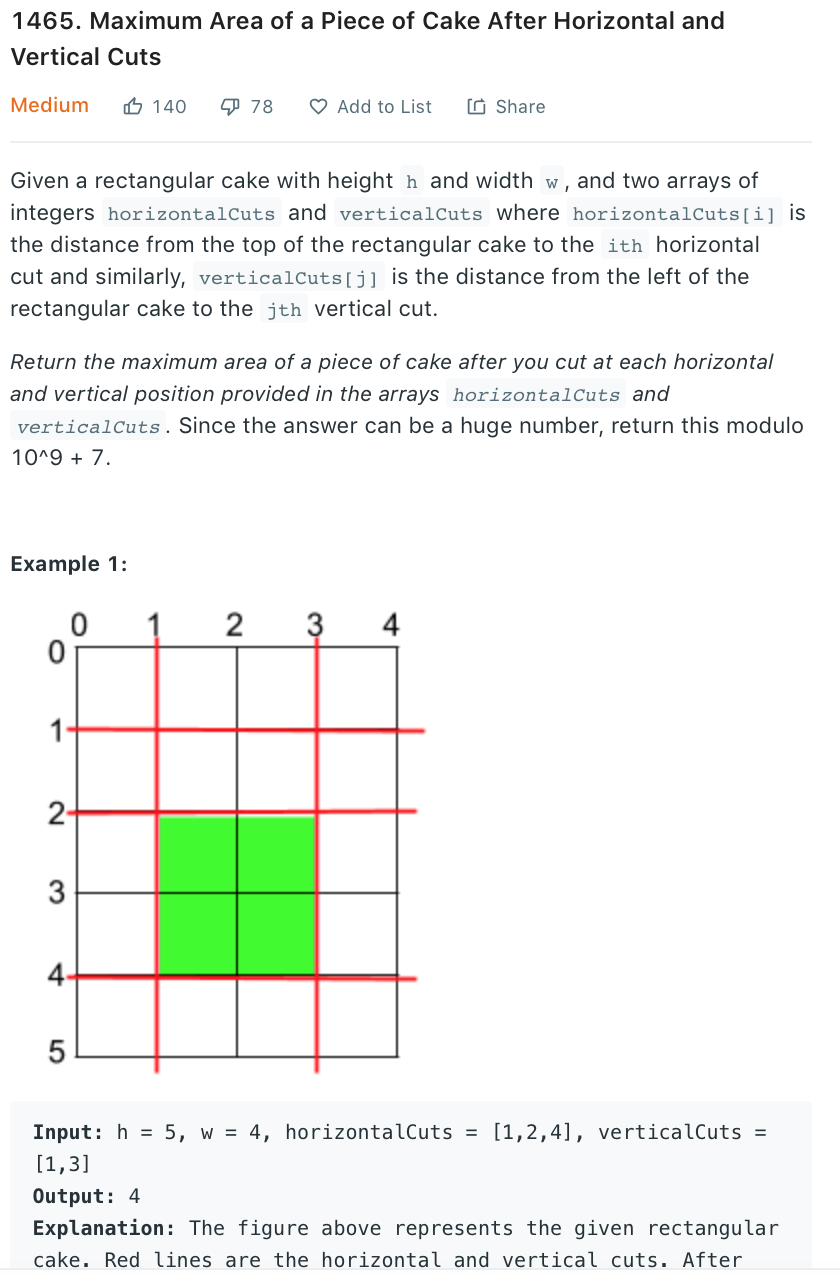
Here's my intial pseudocode:
1. enumerate all the possible areas
2. take the maximum
There were two problems:
Scalability: it's not feasible to calculate every area
Handling of edge cases is unnecessarily complicated, as there are many combinations of inputs (when array is empty, when array has one element, when both arrays are empty etc)
Refer to the code snippet right below; you can see how a lot of codes had to be added just to manage the edge cases. That code passed 51/53 test cases. I think the issue was that I didn't use long as a data type for height and width. At least I passed 51 tests without looking at the answers and discussions!
class Solution {
public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
//intuition: enumerate all the possible areas, and find the maximum one
int max = 0;
Arrays.sort(horizontalCuts);
Arrays.sort(verticalCuts);
for(int i = 0; i<horizontalCuts.length; i++){
int hor2 = horizontalCuts[i];
int hor1 = (i==0)?0:horizontalCuts[i-1];
int height = hor2-hor1;
//edge case where j == verticalCuts.length-1
int tempArea = (w-verticalCuts[verticalCuts.length-1])*height;
if(tempArea>max){max = tempArea;}
//edge case where verticalCuts is empty
if(verticalCuts.length==0){
int tmp = w*height;
max = (tmp>max)?tmp:max;
}
for(int j = 0; j<verticalCuts.length; j++){
int ver2 = verticalCuts[j];
int ver1 = (j==0)?0:verticalCuts[j-1];
int width = ver2-ver1;
int area = (height*width)%((int)(Math.pow(10,9)+7));
if(area>max){
max = area;
}
//edge case where i == horizonalCuts.length-1
int tempArea2 = width*(h-horizontalCuts[horizontalCuts.length-1]);
if(tempArea2>max){max = tempArea2;}
}
}
//edge case where horizontal array is empty
if(horizontalCuts.length == 0){
for(int i = 0; i<verticalCuts.length; i++){
int ver2 = verticalCuts[i];
int ver1 = (i==0)?0:verticalCuts[i-1];
int width = ver2-ver1;
int area = (h*width)%((int)(Math.pow(10,9)+7));
if(area>max){
max = area;
}
}
}
//edge case where both arrays are empty
if(horizontalCuts.length==0&&verticalCuts.length==0){
if(h*w>max){
max = h*w;
}
}
return max;
//for each vertical cut, take its previous cut and find the width
//prev cut is 0 if we are taking the first vertical cut
//for each horizontal cut, take its prev cut and find the height
//prev cut is 0 if we are taking the first horizontal cut
//calculate area by height*width, replace max if greater area found
}
}
So a much better starting point would have been:
1. take the maximum width
2. take the maximum height
3. calculate the area
A major problem that I had, and one that really changed my way of looking at these problems, was finding the maximum interval. The problem gives a length (0 to a given width, w), and gives an array (I'll henceforth call this 'array') that contains points where the length is sliced, and your task is to find the maximum interval. The problem is that there is one more interval than there are elements, and the loop will loop around only array.length times! (if we use int i = 0; i< array.length; i++ that is)
Worse, the code that handles the first and last interval are different from the intervals in between.
So the problem was, I sort of had to come up with a code design that looks like the following
for(int i = 0; iterates one more than array.length times, while 'i' remains meaningful){
1. first interval
2. in between interval
3. last interval
*****do all these while considering the case where the size of given array is 0, 1, or more.
if(interval>max){max = interval}
}
In the solution that I initially came up with, it's clear that I had to add way too many if statements, temporary variables etc. The readability was subpar, I wasn't really aware of whether I was missing any more edge cases.
Here are three things that struck me when I was reading one of the discussion answers.
1. use ternary operator
2. use i<=m
3. use Math.max() - a lot of discussions can be found on this about whether to use this over the if structure or ternary structure, stackoverflow.com/questions/5478877/math-max-vs-inline-if-what-are-the-differences. Concensus seems to be that there is a negligible performance difference, and readability should win the game in that case.
These three things make the code way more readable, easy to understand.
class Solution {
public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
long maxWidth = 0;
long maxHeight = 0;
int m = verticalCuts.length;
int n = horizontalCuts.length;
Arrays.sort(verticalCuts);
Arrays.sort(horizontalCuts);
// get maxWidth
for(int i = 0; i<=m; i++){
maxWidth = Math.max(maxWidth, i==m?w-verticalCuts[i-1]:
(i==0)?verticalCuts[i]:verticalCuts[i]-verticalCuts[i-1]);
}
for(int i = 0; i<=n; i++){
maxHeight = Math.max(maxHeight, i==n?h-horizontalCuts[i-1]:
(i==0)?horizontalCuts[i]:horizontalCuts[i]-horizontalCuts[i-1]);
}
return (int)((maxWidth*maxHeight)%1000000007);
}
}So now, the edge case of when i = m, i = 0 are taken accounted for quite elegantly. Ternary operator allows reusing the same code (that is, maxWidth = Math.max(maxWidth, ...)), as the '...' varies according to whether i ==0 or i==m, or not.
Additionally, knowing that you just had to separately obtain maximum width and maximum height greatly simplified things.