User-based collaborative filtering
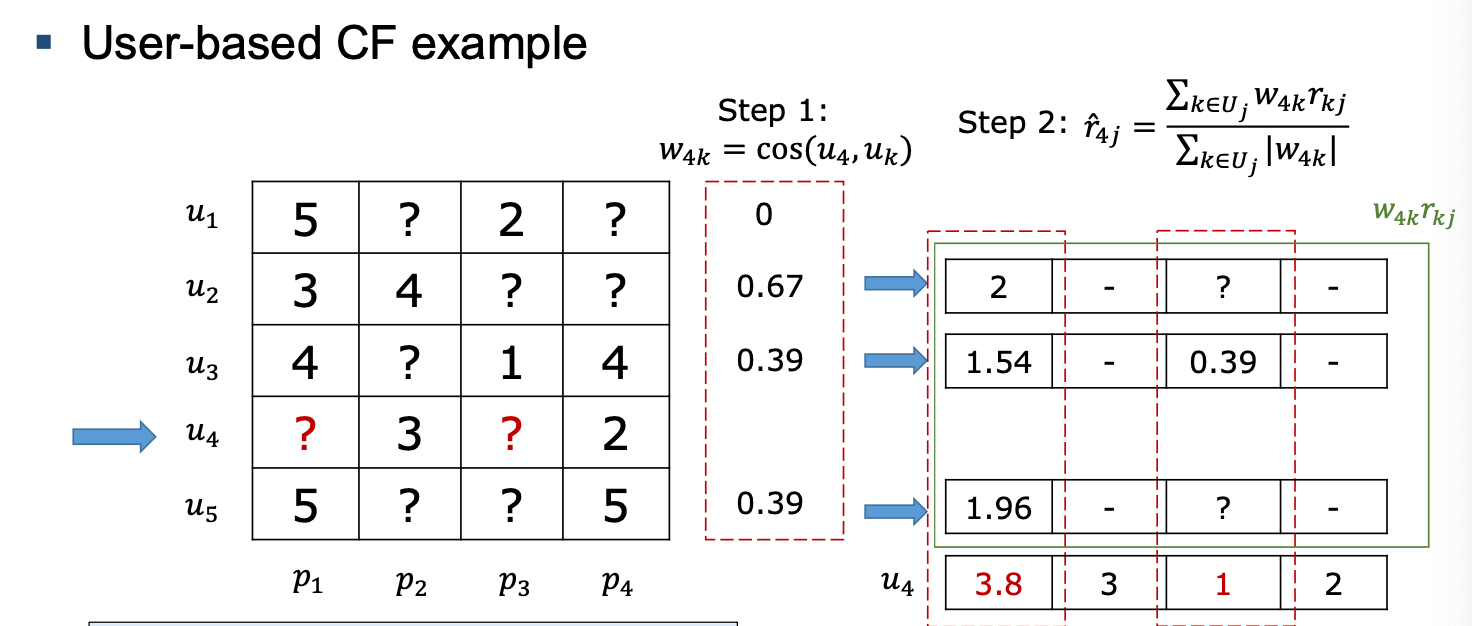
We predict unknown rating of a user based on the ratings of other similar users.
Given a rating matrix, to predict user u's rating on item p by taking a weighted sum of ratings of other users who rated p (either all other users that rated p or top k similar users who rated p). The weight is similarity between u and the other user u', computed based on cosine similarity - cos(u,u'). Take the example of finding u4's missing rating on item p3.
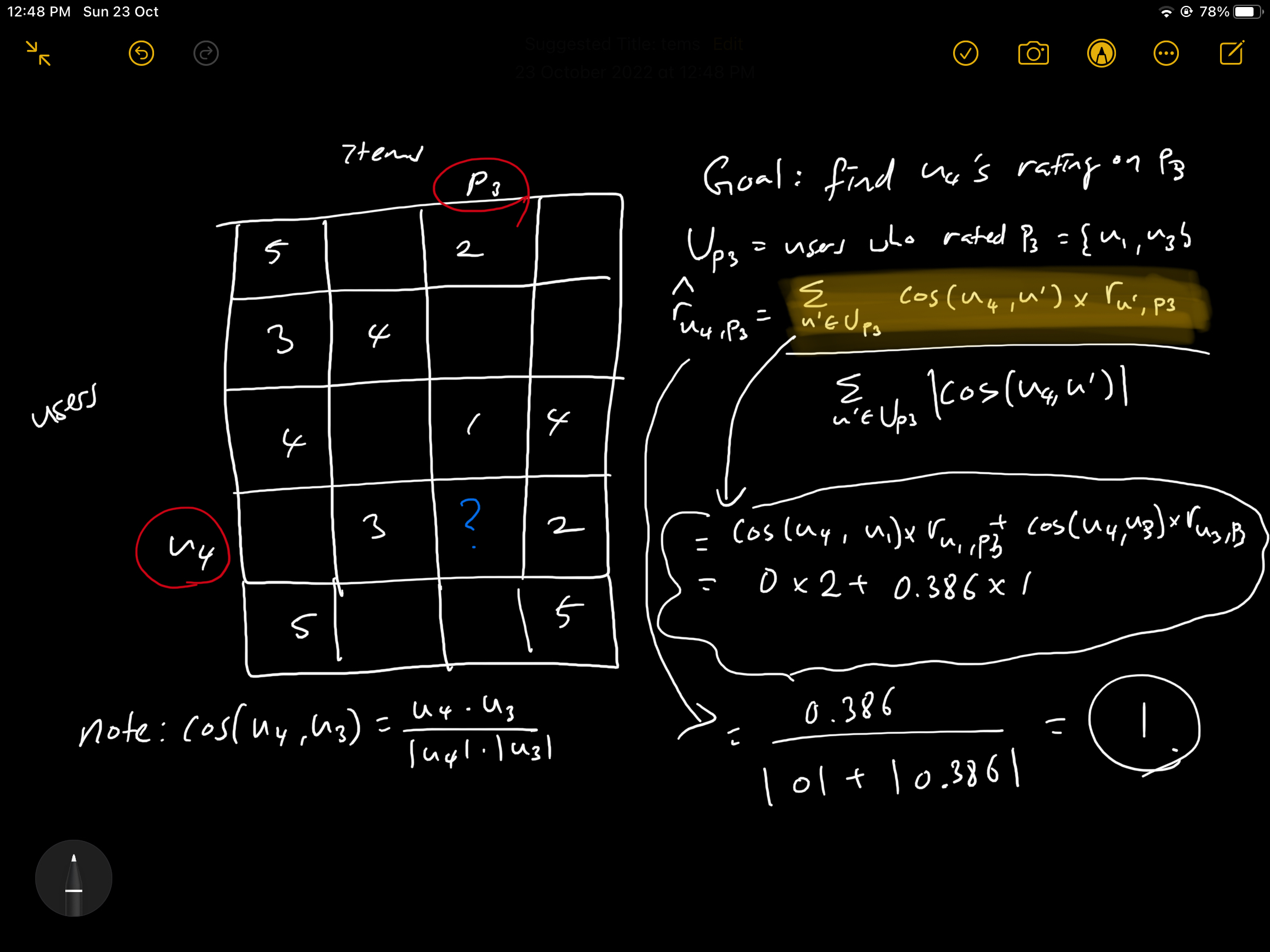
Item-based collaborative filtering
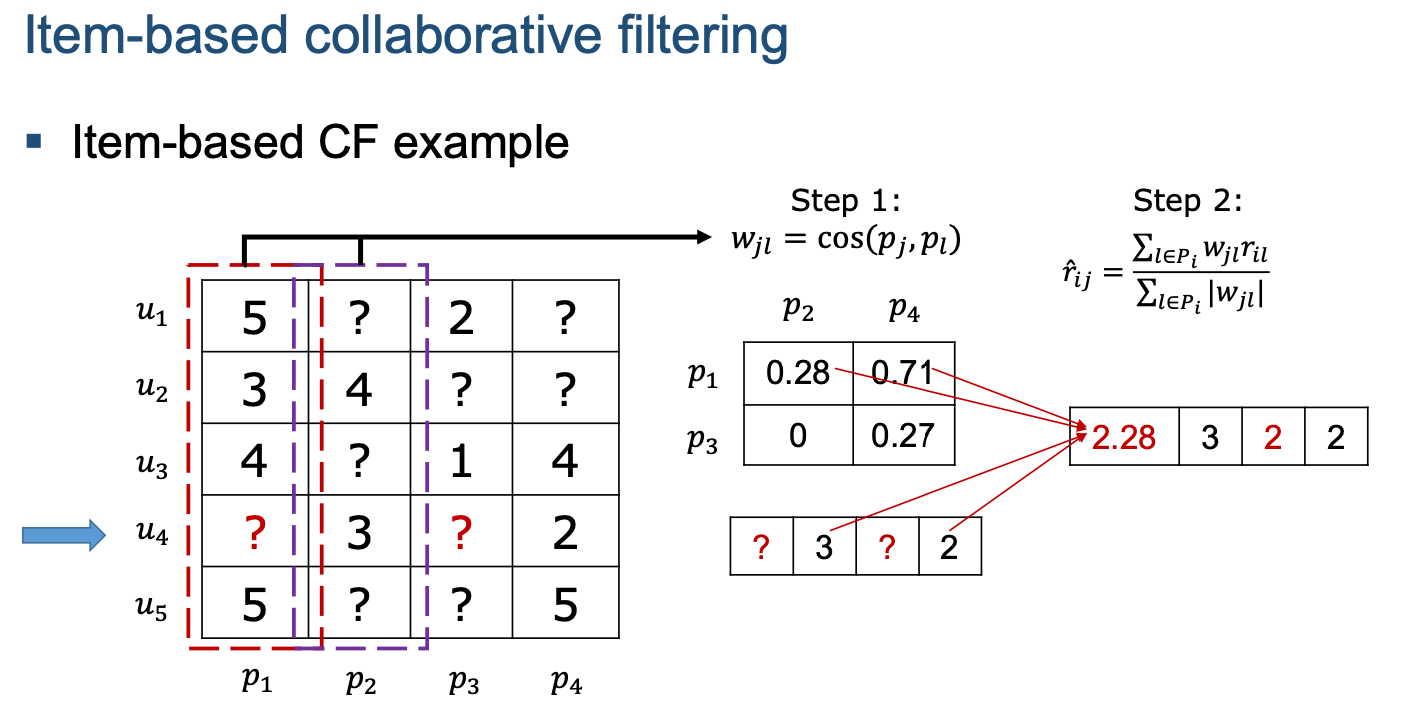
We predict rating of item p by user u based on ratings the user u has given to other items p' (either all or top k similar items).
The following example computes rating of user u4 on item p3 based on lecture example:
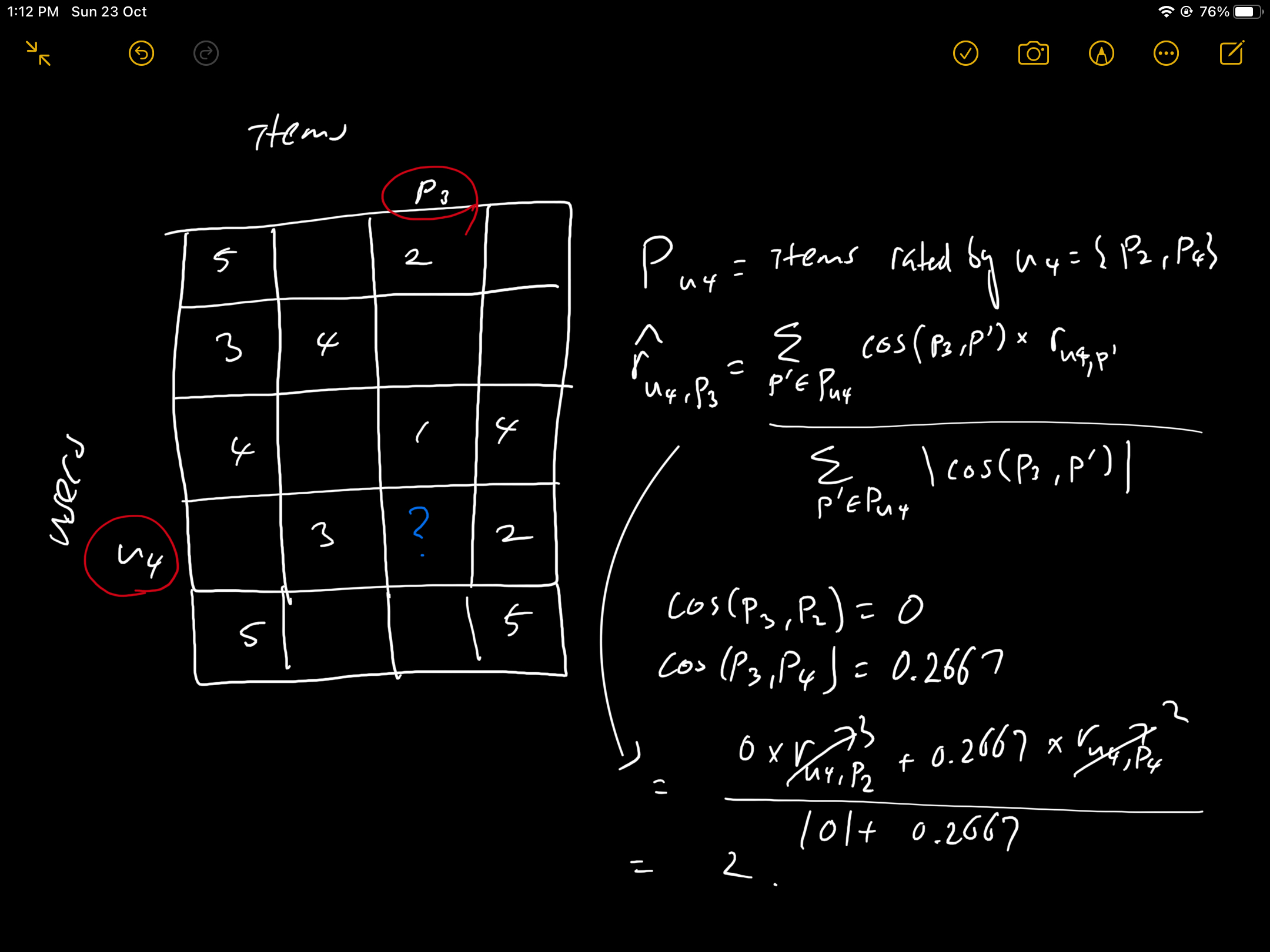
Collaborative filtering with bias terms
Here's a user-based CF with bias terms:

For a better picture, this is what's being done:
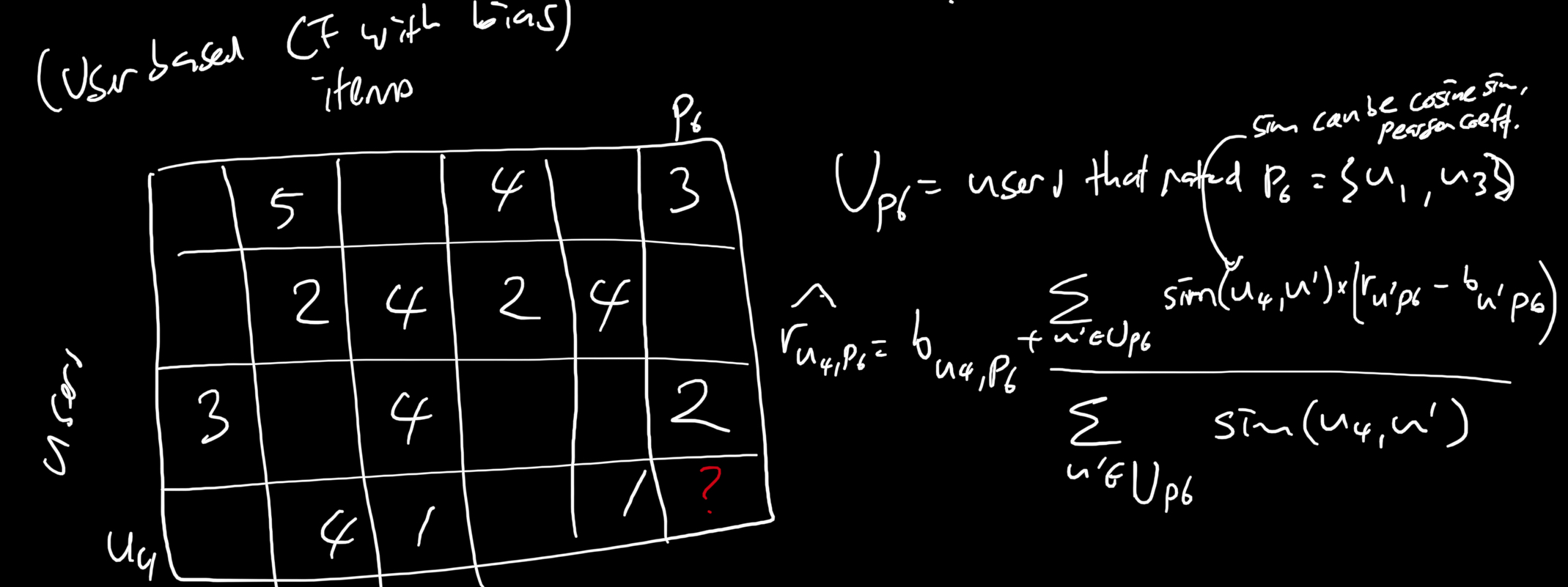
Here's an example of how you would compute user 4's bias on item 6:
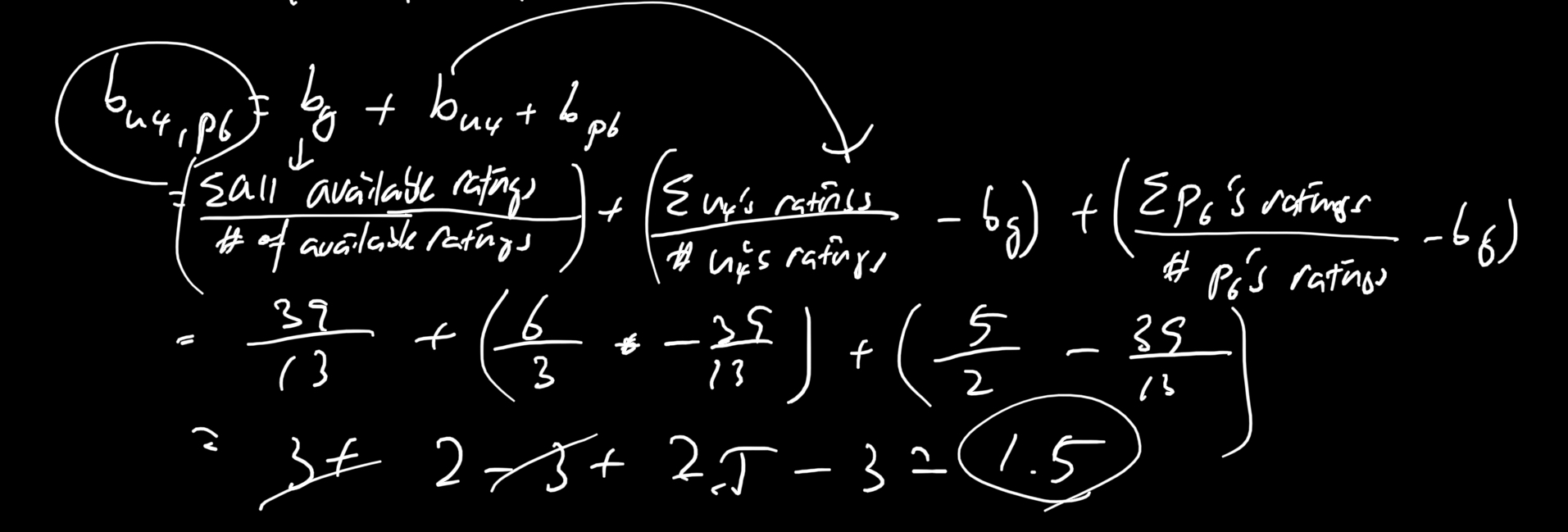
Note: Cosine similarity & Pearson similarity
the exam might specify that I should use pearson correlation as a similiarity measure.
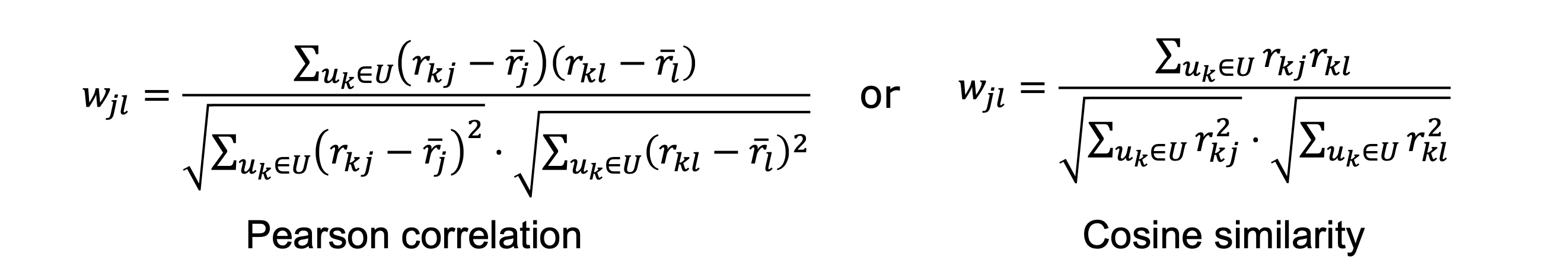
Use this to quickly compute cosine similarity during the exam
import numpy as np
def cosineSim(a,b):
numerator = np.array(a).dot(b)
denom = np.linalg.norm(a)*np.linalg.norm(b)
return numerator/denomHere's pearson similarity
from math import sqrt
def pearsonSim(a,b):
numerator = 0
def getAvg(c):
sum = 0
count = 0
for i in range(len(c)):
if c[i] != 0:
count+=1
sum += c[i]
return sum/count
a_avg = getAvg(a)
b_avg = getAvg(b)
a_denom = 0
b_denom = 0
for i in range(len(a)):
if a[i] != 0 and b[i] != 0:
numerator += (a[i]-a_avg)*(b[i]-b_avg)
a_denom += (a[i]-a_avg)**2
b_denom += (b[i]-b_avg)**2
denom = sqrt(a_denom) * sqrt(b_denom)
return numerator/denom
'2022 > October 2022' 카테고리의 다른 글
| Community detection notes (0) | 2022.10.22 |
|---|---|
| Reservoir Sampling and Bloom Filter notes (0) | 2022.10.19 |
| Universal hashing and minhash notes (0) | 2022.10.18 |


