Independent Cascade notes

1 Independent Cascade (IC)

Influence maximisation tries to pick k nodes that has the greatest influence spread (the number of eventually reached nodes, including the original k nodes).

1.1 Influence spread of seed set S under IC

The procedure of computing influence spread of a seed set S under IC is simple - given a set of nodes, each node has a probability to influence a node. We start with a seed set. Each node in seed set influences a node that it's connected to at a probability p (that probability is independent). Once an influence is taken into account, the node can no longer be part of influence propagation. Here's a rough algorithm illustrating the idea:

 

def IC(seedset):

    queue := seedset

    seen := seedset

    activated := seedset

    while queue is not empty

        temp_queue = empty

        for each node in queue:

            the node activates other nodes with probability associated with edge (and adds it to activated)

            if the other node is not in seen, add it to to temp_queue

        queue = temp_queue

    return activated

 

Influence spread is the number of nodes that have been activated. 

 

HOWEVER this is one case of IC - because the propagation of seedset is probabilistic (hence stochastic). You convert this into deterministic model by enumerating all possible graphs that could have occurred, then calculate IC from each of these graphs, and do a weighted sum to get the true influence spread, which is better representation of what would happen.

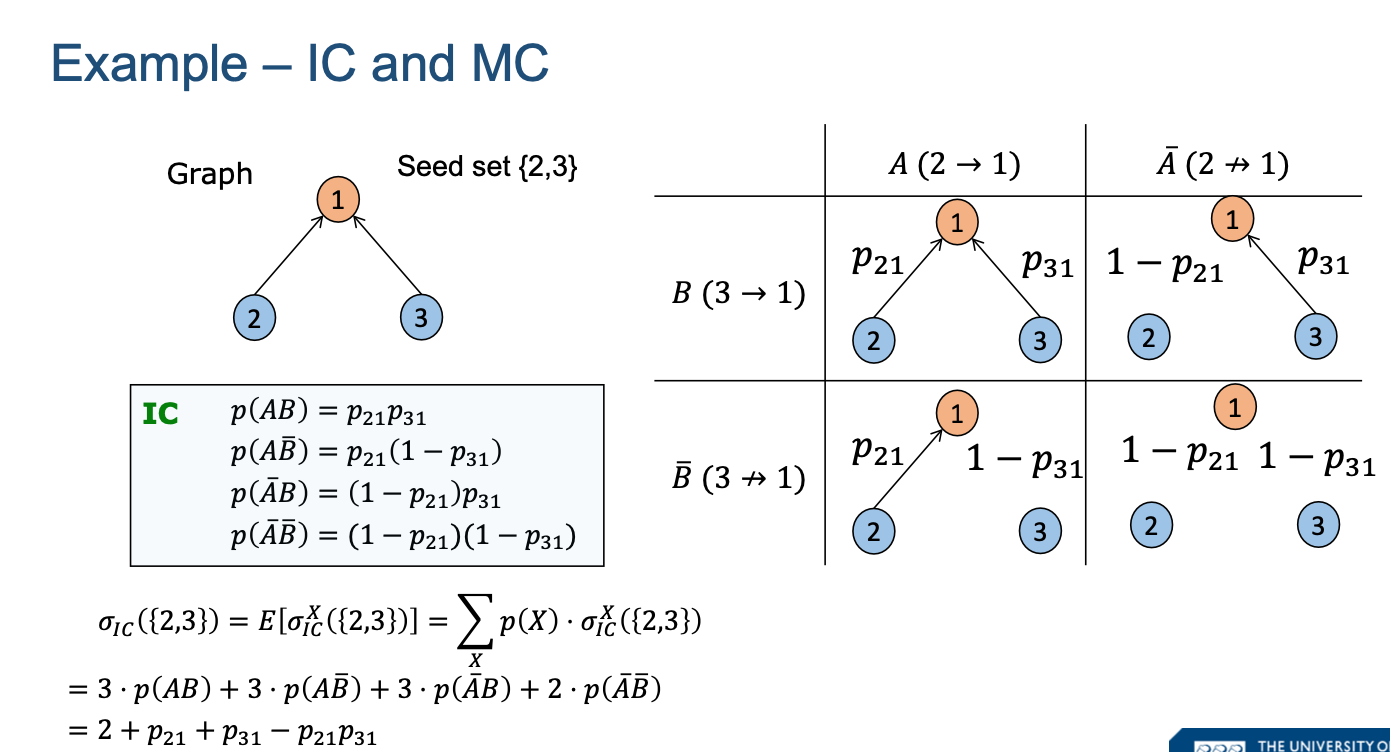
Here, all possible graphs are illustrated in the table. For example, the bottom right graph is showing a case when both nodes in the seedset ({2,3}) failed to influence a node, which happens with a probability of (1-p21)*(1-p31). Each graph has an influence spread (call it s) and a probability of occurrence p (in the case of the bottom right graph, it was (1-p21)*(1-p31)), and we do a weighted sum over these influence spread to get the expected influence spread

1.2 Greedy algorithm for finding seed set with the greatest influence spread

Given section 1.1, we can find influence spread of any seed set. Finding seed set S of k nodes with the greatest resulting influence spread is NP-hard, and instead we approximate it using a greedy algorithm to find S.

 

We start with empty set. While the set is less than k elements, we find one element (not in S) that results in greatest influence spread gain. We do this until we have k elements, and we return S.

However, S is the seed set with greatest influence spread with (1-1/e) probability (e being natural number), ONLY IF the influence spread function (sigma_m()) is non-negative, monotone, submodular. 

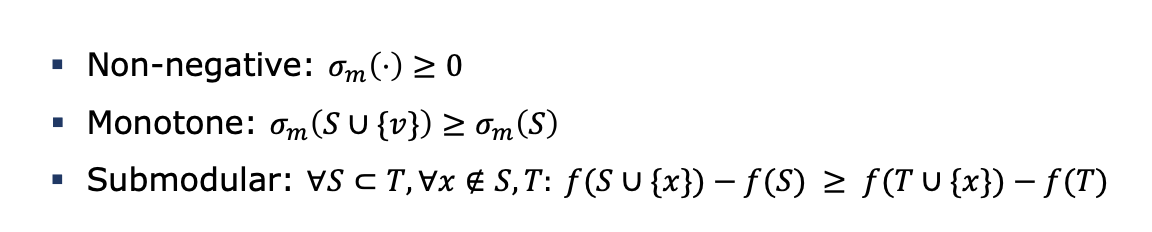
Submodular means that when we have two sets S and T where T is strictly superset of S, we will gain more influence spread by adding an element x (that does not belong to T) to S than to T. 

 

This is consistent with the influence spread function from 1 (proof is that influence spread function on the graph of deterministic graph is submodular, and the expected influence spread function that we derive is a linear combination of influence spread function on deterministic graph, which makes that function deterministic too).